INTEGRAL CALCULUS
Integral Calculus is the branch of calculus where we study integrals and their properties. Integration is an essential concept which is the inverse process of differentiation. Both integral and differential calculus are related to each other by the fundamental theorem of calculus.
If we know the f’ of a function that is differentiable in its domain, we can then calculate f. In differential calculus, we used to call f’, the derivative of the function f. In integral calculus, we call f the anti-derivative or primitive of the function f’. And the process of finding the anti-derivatives is known as anti-differentiation or integration.
Integration can be classified into two different categories, namely,
- Definite Integral
- Indefinite Integral
e name suggests, it is the inverse of finding differentiation.
Definite Integral
An integral that contains the upper and lower limits (i.e.) start and end value is known as a definite integral. The value of x is restricted to lie on a real line, and a definite Integral is also called a Riemann Integral when it is bound to lie on the real line.
A definite Integral is represented as:
Learn more about definite integrals here.
Indefinite Integral
Indefinite integrals are not defined using the upper and lower limits. The indefinite integrals represent the family of the given function whose derivatives are f, and it returns a function of the independent variable.
The integration of a function f(x) is given by F(x) and it is represented by:
∫f(x) dx = F(x) + C
where R.H.S. of the equation means integral off(x) with respect to x
F(x) is called anti-derivative or primitive.
f(x) is called the integrand.
dx is called the integrating agent.
C is called the constant of integration.
x is the variable of integration.
Click here to understand more about indefinite integral.
It may seem strange that there exist an infinite number of anti-derivatives for a function f. Taking an example will clarify it. Let us take f’ (x) = 3x2. By hit and trial, we can find out that its anti-derivative is F(x) = x3. This is because if you differentiate F with respect to x, you will get 3x2. There is only one function that we got as the anti-derivative of f. Let us now differentiate G(x)= x3 + 9 with respect to x. Again we would get the same derivative, i.e. f. This gives us an important insight. Since the differentiation of all the constants is zero, we can write any constant with x3, and the derivative would still be equal to f. So, there are infinite constants that can be substituted for c in the equation F(x) = x3 + C. Hence, there are infinite functions whose derivative is equal to f. And hence, there are infinite functions whose derivative is equal to 3x2. C is called an arbitrary constant. It is sometimes also referred to as the constant of integration.
☛ Also Check:
THIS IS A BRAVE ATTEMPT TO HELP ALL STUDENTS GET QUALITY STUDY MATERIAL FOR FREE.HOPE YOU APPRECIATE
☛ Also Check:
Integral Calculus Examples
A Practical Example: Tap and Tank
Now For An Increasing Flow Rate
Other functions
Example: what is ∫cos(x) dx ?
Example: What is ∫x3 dx ?
Definite vs Indefinite Integrals
What is Integral Calculus Used for?
Integral Calculus Formulas
What are the Applications of Integral Calculus?
Solved Examples
Summary
Frequently Asked Questions
.
integral Calculus Formulas
Similar to differentiation formulas, we have integral formulas as well. Let us go ahead and look at some of the integral calculus formulas.
Methods of Finding Integrals of Functions
We have different methods to find the integral of a given function in integral calculus. The most commonly used methods of integration are:
It is also possible to integrate the given function using the partial fractions technique.
Uses of Integral Calculus
Integral Calculus is mainly used for the following two purposes:
- To calculate f from f’. If a function f is differentiable in the interval of consideration, then f’ is defined. In differential calculus, we have already seen how to calculate derivatives of a function, and we can “undo” that with the help of integral calculus.
- To calculate the area under a curve.
Application of Integral Calculus
Find the integral of cos2n with respect to n.
Solution:
Let f(n) = cos2n
we know that 2 cos2A = cos 2A + 1
So, f(n) = (1/2)(cos 2n + 1)
Let us find the integral of f(n).
∫f(n) dn = ∫(1/2)(cos 2n + 1) dn
= (1/2) ∫(cos 2n + 1) dn
= (1/2) ∫cos 2n dn + (1/2)∫1 dn
= (1/2) (sin 2n/2) + (1/2) n + C
= (sin 2n/4) + (n/4) + C
(1/4)[sin 2n + n] + C
Fundamental Theorems of Integral Calculus
We define integrals as the function of the area bounded by the curve y = f(x), a ≤ x ≤ b, the x-axis, and the ordinates x = a and x =b, where b>a. Let x be a given point in [a,b]. Then represents the area function. This concept of area function leads to the fundamental theorems of integral calculus.
- First Fundamental Theorem of Integral Calculus
- Second Fundamental Theorem of Integral Calculus
First Fundamental Theorem of Integrals
A(x) = for all x ≥ a, where the function is continuous on [a,b]. Then A'(x) = f(x) for all x ϵ [a,b]
Second Fundamental Theorem of Integrals
If f is continuous function of x defined on the closed interval [a,b] and F be another function such that d/dx F(x) = f(x) for all x in the domain of f, then = f(b) -f(a). This is known as the definite integral of f over the range [a,b], a being the lower limit and b the upper limit.
Types of Integrals
Integral calculus is used for solving the problems of the following types.
a) the problem of finding a function if its derivative is given.
b) the problem of finding the area bounded by the graph of a function under given conditions. Thus the Integral calculus is divided into two types.
- Definite Integrals (the value of the integrals are definite)
- Indefinite Integrals (the value of the integral is indefinite with an arbitrary constant, C)
Indefinite Integrals
These are the integrals that do not have a pre-existing value of limits; thus making the final value of integral indefinite. ∫g'(x)dx = g(x) + c. Indefinite integrals belong to the family of parallel curves.
Definite Integrals
The definite integrals have a pre-existing value of limits, thus making the final value of an integral, definite. if f(x) is a function of the curve, then
properties of Integral Calculus
Let us study the properties of indefinite integrals to work on them.
- The derivative of an integral is the integrand itself. ∫ f(x) dx = f(x) +C
- Two indefinite integrals with the same derivative lead to the same family of curves and so they are equivalent. ∫ [ f(x) dx -g(x) dx] =0
- The integral of the sum or difference of a finite number of functions is equal to the sum or difference of the integrals of the individual functions. ∫ [ f(x) dx+g(x) dx] = ∫ f(x) dx + ∫ g(x) dx
- The constant is taken outside the integral sign. ∫ k f(x) dx = k ∫ f(x) dx, where k ∈ R.
- The previous two properties are combined to get the form: ∫ [kf(x) + kf(x) +... kf(x)] dx = k∫ f(x)dx + k∫ f(x)dx+ ... k ∫ f(x)dx
Integrals Formulas
We can remember the formulas of derivatives of some important functions. Here are the corresponding integrals of these functions that are remembered as standard formulas of integrals.
- ∫ xn dx=xn+1 /n+1+C, where n ≠ -1
- ∫ dx =x+C
- ∫ cosxdx = sinx+C
- ∫ sinx dx = -cosx+C
- ∫ sec2x dx = tanx+C
- ∫ cosec2x dx = -cotx+C
- ∫ sec2x dx = tanx+C
- ∫ secx tanxdx = secx+C
- ∫ cscx cotx dx = -cscx+C
- ∫1/(√(1-x2))= sin-1 x + C
- ∫-1/(√(1-x2))= cos-1 x + C
- ∫1/(1+x2)= tan-1 x + C
- ∫-1/(1+x2)= cot-1 x + C
- ∫1/(x√(x2 -1))= sec-1 x + C
- ∫-1/(x√(x2 -1))= cosec-1 x + C
- ∫ exdx=ex + C
- ∫dx/x=ln|x| + C
- ∫ ax dx=ax/ln a + C
Methods to Find Integrals
There are several methods adopted for finding the indefinite integrals. The prominent methods are:
- Finding integrals by integration by substitution method
- Finding integrals by integration by parts
- Finding integrals by integration by partial fractions.
Finding Integrals by Substitution Method
A few integrals are found by the substitution method. If u is a function of x, then u' = du/dx.
∫ f(u)u' dx = ∫ f(u)du, where u = g(x).
Finding Integrals by Integration by Parts
If two functions are of the product form, integrals are found by the method of integration by parts.
∫f(x)g(x) dx = f(x)∫ g(x) dx - ∫ (f'(x) ∫g(x) dx) dx.
Finding Integrals by Integration by Partial Fractions
Integration of rational algebraic functions whose numerator and denominator contain positive integral powers of x with constant coefficients is done by resolving them into partial fractions.
To find ∫ f(x)/g(x) dx, decompose this improper rational function to a proper rational function and then integrate.
∫f(x)/g(x) dx = ∫ p(x)/q(x) + ∫ r(x)/s(x), where g(x) = a(x) . s(x)
Applications of Integral Calculus
Using integration, we can find the distance given the velocity. Definite integrals form the powerful tool to find the area under simple curves, the area bounded by a curve and a line, the area between two curves, the volume of the solids. The displacement and motion problems also find their applications of integrals. The area of the region enclosed between two curves y = f(x) and y = g(x) and the lines x =a, x =b is given by
Area =
Let us find the area bounded by the curve y = x and y = x2 that intersect at (0,0)and (1,1).
The given curves are that of a line and a parabola. The area bounded by the curves =
Area =
= x2 /2- x 3/3
= 1/2-1/3
= 1/6 sq units.
Important Notes
- The primitive value of the function found by the process of integration is called an integral.
- An integral is a mathematical object that can be interpreted as an area or a generalization of area.
- When a polynomial function is integrated the degree of the integral increases by 1.
Properties of Indefinite Integral
(i) ∫[f(x) + g(x)] dx = ∫f(x) dx + ∫g(x) dx
(ii) For any real number k, ∫k f(x) dx = k∫f(x)dx.
(iii) In general, if f1, f2,………, fn are functions and k1, k2,…, kn are real numbers, then
∫[k1f1(x) + k2 f2(x)+…+ knfn(x)] dx = k1 ∫f1(x) dx + k2 ∫ f2(x) dx+…+ kn ∫fn(x) dx
Basic Formulae

Integration using Trigonometric Identities
When the integrand involves some trigonometric functions, we use the following identities to find the integral:
- 2 sin A . cos B = sin( A + B) + sin( A – B)
- 2 cos A . sin B = sin( A + B) – sin( A – B)
- 2 cos A . cos B = cos (A + B) + cos(A – B)
- 2 sin A . sin B = cos(A – B) – cos (A + B)
- 2 sin A cos A = sin 2A
- cos2 A – sin2 A = cos 2A
- sin2 A = (
1−cos2A2 ) - sin2 A + cos2 A = 1
sin3A=3sinA−sin3A4 cos3A=3cosA+cos3A4
Integration by Substitutions
Substitution method is used, when a suitable substitution of variable leads to simplification of integral.
If I = ∫f(x)dx, then by putting x = g(z), we get
I = ∫ f[g(z)] g'(z) dz
Note: Try to substitute the variable whose derivative is present in the original integral and final integral must be written in terms of the original variable of integration.
Integration by Parts
For a given functions f(x) and q(x), we have
∫[f(x) q(x)] dx = f(x)∫g(x)dx – ∫{f'(x) ∫g(x)dx} dx
Here, we can choose the first function according to its position in ILATE, where
I = Inverse trigonometric function
L = Logarithmic function
A = Algebraic function
T = Trigonometric function
E = Exponential function
[the function which comes first in ILATE should taken as first junction and other as second function]
Note
(i) Keep in mind, ILATE is not a rule as all questions of integration by parts cannot be done by above method.
(ii) It is worth mentioning that integration by parts is not applicable to product of functions in all cases. For instance, the method does not work for ∫√x sinx dx. The reason is that there does not exist any function whose derivative is √x sinx.
(iii) Observe that while finding the integral of the second function, we did not add any constant of integration.
Integration by Partial Fractions
A rational function is ratio of two polynomials of the form


where x2 + bx + c cannot be factorised further.

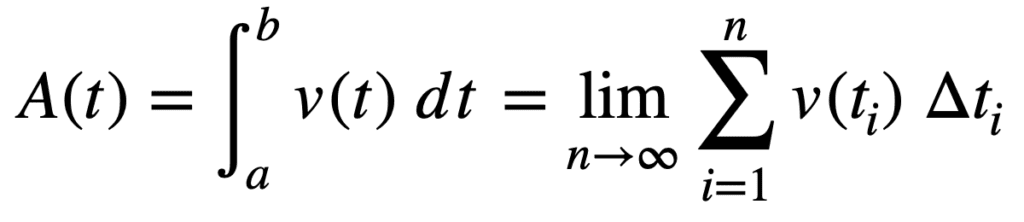














No comments:
Post a Comment