FUNCTIONS

                        

 Functions

What are Functions in Mathematics?

A function is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output. Let A & B be any two non-empty sets; mapping from A to B will be a function only when every element in set A has one end, only one image in set B.

Another definition of functions is that it is a relation “f” in which each element of set “A” is mapped with only one element belonging to set “B”. Also in a function, there can’t be two pairs with the same first element.

A Condition for a Function:

Set A and Set B should be non-empty.

In a function, a particular input is given to get a particular output. So, A function f: A->B denotes that f is a function from A to B, where A is a domain and B is a co-domain.

• For an element, a, which belongs to A, a ∈ A, a unique element b, b ∈ B is there such that (a,b) ∈ f.

The unique element b to which f relates a, is denoted by f(a) and is called f of a, or the value of f at a, or the image of a under f.

• The range of f (image of a under f)
• It is the set of all values of f(x) taken together.
• Range of f = { y ∈ Y | y = f (x), for some x in X}

A real-valued function has either P or any one of its subsets as its range. Further, if its domain is also either P or a subset of P, it is called a real function.

Vertical Line Test:

Vertical line test is used to determine whether a curve is a  function or not. If any curve cuts a vertical line at more than one points then the curve is not a function.

Representation of Functions

Functions are generally represented as f(x).

Let , f(x) = x3.

It is said as f of x is equal to x cube.

Functions can also be represented by g(), t(),… etc.

Steps for Solving Functions

Question: Find the output of the function g(t) = 6t2 + 5 at

(i) t = 0

(ii) t = 2

Solution:

The given function is g(t) = 6t2 + 5

(i) At t = 0, g(0) = 6(0)2 + 5 = 5

(ii) At t = 2, g(2) = 6(2)2 + 5 = 29

Types of Functions

There are various types of functions in mathematics which are explained below in detail. The different function types covered here are:

• One – one function (Injective function)
• Many – one function
• Onto – function (Surjective Function)
• Into – function
• Polynomial function
• Linear Function
• Identical Function
• Quadratic Function
• Rational Function
• Algebraic Functions
• Cubic Function
• Modulus Function
• Signum Function
• Greatest Integer Function
• Fractional Part Function
• Even and Odd Function
• Periodic Function
• Composite Function
• Constant Function
• Identity Function

Many One Function

Many one function is an important function which relates two or more elements of the domain set with a single element of the codomain set. Many one function is a function f: x→ y such that two or more elements of the set x are related to a single element of the set y.

Let us learn more about many one function, properties of many one function, with examples, FAQs.

What Is Many One Function?

Many one function is a function in which two or more elements of a set are connected to a single element of another set. The function f: x → y, such that two or more elements in the domain of the function f and belonging to the set x are connected to a single element in the codomain of the function f and belonging to the set y. Here two or more two elements of the domain are connected with the same element in the codomain.

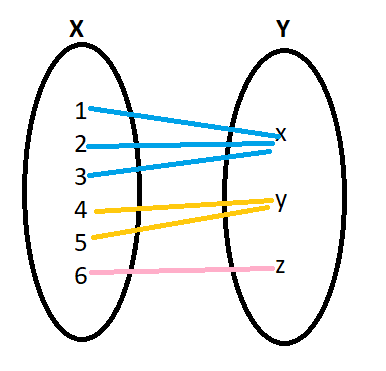
Let us consider an example with two sets with the set A = {1, 2, 3, 4, 5} as the domain, and the Set B = {x, y, z} as the range. Here the function f from A to B is said to be many one function, if we have f = {(1, x), (2, x), (3, x), (4, y), (5, z)}.

The many one functions can also be called a constant function if all the elements of the domain are connected to only one element in the codomain. And the many one function is called an onto function if each element in the range has been utilized.

Properties Of Many One Function

The following are some of the important properties of many one function.

• The domain of the function should have at least two elements having the same codomain value.
• The number of elements in the domain of many one functions is more than the number of elements in the codomain.
• The codomain of the many one functions has the same value for more than one domain value.
• The codomain of many one functions is always lesser than the range value.
• The many one function can also be called a constant function if there is only one codomain.

Related Topics

The following topics help in a better understanding of many one functions

• Increasing and Decreasing Functions
• Relations and Functions
• Even and Odd Functions
• Types of Functions
• Trigonometric Functions
• Logarithmic Functions

 

Examples on Many One Function

1. Example 1: Find the domain and range of the many one function f = {(1, a), (2, a), (3, a), (4, b), (5, b), (6, c)}

   Solution:

   The given function is f = {(1, a), (2, a), (3, a), (4, b), (5, b), (6, c)}

   Here we have:

   Domain = (1, 2, 3, 4)

   Range = (a, b, c)

   We observe that the elements 1, 2, 3, in the domain are all connected to the same element 'a' in the range set. Hence we see that this function connecting the elements of th domain set to the element in the range set, makes a many one function.

   Therefore, the given function is many one function.

2. Example 2: Prove that the function f(x) = x² is an onto function.

   Solution:

   The given function if f(x) = x². Let us take a few values for the domain of this function and find the range, and then try and understand the type of this function.

   Let x = 2, f(2) = 2² = 4

   For x = -2, f(-2) = (-2)² = 4

   x = 3, f(3) = 3² = 9

   x = -3, f(-3) = (-3)² = 9.

   For the elements of x = 2, -2, the f(x) value is 4, and for the values of x = 3, -3, the range is 9.

   Therefore, the function f(x) = x² is a many one function.

3. Hint: As we know that a function f:X→Y$f:X\to Y$ that is from variable X$X$ to variable Y$Y$ is said to be one-one functions if there exist only one element from domain connected with only one and unique element from co-domain. Similarly ,we can say that a functionf:X→Y$f:X\to Y$ that is from variable X$X$ to variable Y$Y$ is said to be many-one functions if there exist two or more elements from the domain connected with the same element from the co-domain.
   With the help of this definition, we can give an example, consider elements of X$X$ be {1,2}$\{1,2\}$ and elements of Y$Y$ be {x}$\{x\}$ and f:X→Y$f:X\to Y$ such that f={(1,x),(2,x)}$f=\{(1,x),(2,x)\}$ . here element one and two both connected with the same element that is x$x$ . This is how a function can have many-one relationships.
   
   Complete step-by-step answer:
   Many-one function is defined as , A functionf:X→Y$f:X\to Y$ that is from variable X$X$ to variable Y$Y$ is said to be many-one functions if there exist two or more elements from a domain connected with the same element from the co-domain .
   Let us consider an example ,
   Let the domain or elements of X$X$ be {1,2.3,4,5,6}$\{1,2.3,4,5,6\}$ ,
   Let the co-domain or elements of Y$Y$ be {x,y,z}$\{x,y,z\}$ and
   f:X→Y$f:X\to Y$
   Such that f={(1,x),(2,x),(3,x),(4,y),(5,z)}$f=\{(1,x),(2,x),(3,x),(4,y),(5,z)\}$
   

   

   
   Here elements one , two and three all are connected with the same element that is x$x$ , and the elements four and five are connected with the same element that is y$y$. This is how a function can have many-one relationships.
   
   Note: Range is defined as the set of elements from y$y$ that actually come out whereas the co-domain of a function is given by the set of values that can possibly become a range of the function. In this particular question the range of the function is equal to the co-domain of the function.

4. The functional notation f (x) literally means “function of x”.
   
   
   
   

   Ways of expressing a function

   A function can be expressed in various ways:
   
   

   • A function can be expressed in list form, especially if the domain and range are small. Here is an example of a function in list form:
     
     

     domain	range
     10	3
     2	15
     5	46

     If this function is called f then f (10) = 3 and f (2) = 15.
     
     
   
   
   • A function can be expressed in graph form. The function is represented by a curve drawn on a cartesian plane. The domain is plotted horizontally (in the x direction) and the range is plotted vertically (in the y direction). To find the range value y corresponding to a given domain value x you start at the domain value on the x axis, go vertically until you reach the graph, then go horizontally until you reach the y axis. Here is an example of a function in graph form:
     
     
     
     
     
     If this function is called g then for example g (−1) = 1 and g (2) = 2.5. Click here to see the graphs of a variety of function types.
     
     
   
   
   • A function can be expressed in formula form. The formula is used to calculate the range value for any given domain value. Here is an example of a function in formula form:

     h (x) = x ² − 2 x

     This function is called h . Here is an example showing how the formula is used to calculate a value of the range for a value of the domain, say 4. The domain value 4 is substituted in for x wherever x occurs and then the formula is simplified to yield the range value:

     h (4) = 4 ² − 2 · 4 = 8.

     Here is another example with the domain value 5:

     h (5) = 5 ² − 2 · 5 = 15.

     
     Another way to write the above function is this:

     y = x ² − 2 x.

     In this form h (x) has been replaced by a new variable y so that there are now two variables, x and y. Variable y is the value of the range that corresponds to the value of variable x of the domain. Variable y is called the dependent variable and variable x is called the independent variable. This form plays down the function aspect of the relationship and just gives an equation connecting values of the domain and range. Yet another way to write the function is in two parts, like this:

     y = h (x), where h (x) = x ² − 2 x.

     The first part gives a name to the function and the second part gives the formula for the function.
     
     
     

   ---

   
   

   The argument and value of a function

   The value of the domain that goes into the function machine is also called the argument of the function and the value of the range that comes out of the function machine is also called the value of the function. For example suppose that f (5) = 15. Then we say that the argument of the function f is 5 and the value of f is 15.
   
   

   

   
   
   

   ---

   
   

   Identifying the domain and range of a function

   The domain and range of a function isn’t always the set of all real numbers. If a function is expressed in list or graph form you can identify the domain and range by simply looking at the list or graph. But if the function is expressed in formula form then you must do the following:

   • Substitute potential domain values into the formula and make sure that they don’t cause an undefined operation to occur (such as division by zero or the square root of a negative number). If they do then they are not in the domain.
     
     
   • Once the domain is known, you can find the range by substituting various domain value into the formula.

   • Constant Function:
     Let ‘A’ and ‘B’ be any two non–empty sets, then a function ‘f$f$’ from ‘A’ to ‘B’ is called a constant function if and only if the range of ‘f$f$’ is a singleton.

     Algebraic Function:
     A function defined by an algebraic expression is called an algebraic function.
     e.g. f(x)=x2+3x+6$f\left(\text{x}\right)={\text{x}}^2+3\text{x}+6$

     Polynomial Function:
     A function of the form P(x)=amxn+an–1xn–1+⋯+a1x+a0$\text{P}\left(\text{x}\right)={\text{a}}_{\text{m}}{\text{x}}^{\text{n}}+{\text{a}}_{\text{n}–1}{\text{x}}^{\text{n}–1}+\cdots +{\text{a}}_1\text{x}+{\text{a}}_0$
     where ‘n’ is a positive integer and an,an–1,⋯,a1,a0${\text{a}}_{\text{n}},{\text{a}}_{\text{n}–1},\cdots ,{\text{a}}_1,{\text{a}}_0$ are real numbers is called a polynomial function of degree ‘n’.

     Linear Function:
     A polynomial function with degree ‘t$t$’ is called a linear function. The most general form of a linear function is
     f(x)=ax+b$f\left(\text{x}\right)=\text{ax}+\text{b}$

     Quadratic Function:
     A polynomial function with degree ‘2’ is called a quadratic function. The most general form of a quadratic equation is f(x)=ax2+bx+c$f\left(\text{x}\right)=\text{a}{\text{x}}^2+\text{bx}+\text{c}$

     Cubic Function:
     A polynomial function with degree ‘3’ is called a cubic function. The most general form of a cubic function is f(x)=ax3+bx2+cx+d$f\left(\text{x}\right)=\text{a}{\text{x}}^3+\text{b}{\text{x}}^2+\text{cx}+\text{d}$

     Identity Function:
     Let f:A→B$f:\text{A}\to \text{B}$ be a function then ‘f$f$’ is called an identity function if f(x)=x,∀x∈A$f\left(\text{x}\right)=\text{x,}\mathrm{\forall }\text{x}\in \text{A}$.

     Rational Function:
     A function R(x)$R\left(\text{x}\right)$ defined by R(x)=P(x)Q(x)$R\left(\text{x}\right)=\frac{\text{P}\left(\text{x}\right)}{\text{Q}\left(\text{x}\right)}$, where both P(x)$\text{P}\left(\text{x}\right)$andQ(x)$\text{Q}\left(\text{x}\right)$ are polynomial functions is called a rational function.

     Trigonometric Function:
     A function f(x)=sinx$f\left(\text{x}\right)=\sin \text{x}$, f(x)=cosx$f\left(\text{x}\right)=\cos \text{x}$ etc., then f(x)$f\left(\text{x}\right)$ is called a trigonometric function.

     Exponential Function:
     A function in which the variable appears as an exponent (power) is called an exponential function
     e.g. (i) f(x)=ax$f\left(\text{x}\right)={\text{a}}^{\text{x}}$ (ii) f(x)=3x$f\left(\text{x}\right)=3^{\text{x}}$.